Can All Matrices a Ã¢ë†ë† R^nãƒâ€”n Be Factored a = Lu

LU decomposition of a matrix is the factorization of a given square matrix into two triangular matrices, i upper triangular matrix and ane lower triangular matrix, such that the product of these two matrices gives the original matrix. Information technology was introduced by Alan Turing in 1948, who as well created the Turing car.

This method of factorizing a matrix every bit a product of two triangular matrices has diverse applications such as a solution of a organization of equations, which itself is an integral part of many applications such as finding current in a excursion and solution of detached dynamical arrangement problems; finding the inverse of a matrix and finding the determinant of the matrix.
Basically, the LU decomposition method comes in handy whenever it is possible to model the trouble to be solved into matrix grade. Conversion to the matrix grade and solving with triangular matrices makes information technology easy to practice calculations in the process of finding the solution.

A foursquare matrix A tin be decomposed into 2 square matrices L and U such that A = L U where U is an upper triangular matrix formed as a outcome of applying the Gauss Elimination Method on A, and Fifty is a lower triangular matrix with diagonal elements being equal to ane.

For A = 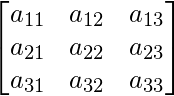$\begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix}$ , we have L = 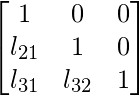$\begin{bmatrix} 1 & 0 & 0 \\ l_{21} & 1 & 0 \\ l_{31} & l_{32} & 1 \end{bmatrix}$ and U = 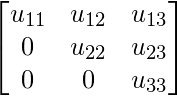$\begin{bmatrix} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & u_{33} \end{bmatrix}$ ; such that A = L U.

$\left[\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right]=\left[\begin{array}{lll} 1 & 0 & 0 \\ l_{21} & 1 & 0 \\ l_{31} & l_{32} & 0 \end{array}\right] *\left[\begin{array}{ccc} u_{11} & u_{12} & u_{13} \\ 0 & u_{22} & u_{23} \\ 0 & 0 & u_{33} \end{array}\right]$

Hither value of 50₂₁ , u_xi etc can be compared and plant.

Gauss Elimination Method
According to the Gauss Emptying method:

Whatever zero row should be at the bottom of the matrix.
The offset non naught entry of each row should be on the correct-mitt side of the first not nada entry of the preceding row. This method reduces the matrix to row echelon form.

Steps for LU Decomposition:

Given a set of linear equations, kickoff convert them into matrix grade A X = C where A is the coefficient matrix, Ten is the variable matrix and C is the matrix of numbers on the right-hand side of the equations.
At present, reduce the coefficient matrix A, i.due east., the matrix obtained from the coefficients of variables in all the given equations such that for 'n' variables we have an nXn matrix, to row echelon form using Gauss Elimination Method. The matrix so obtained is U.
To discover L, we take two methods. The starting time i is to assume the remaining elements as some artificial variables, make equations using A = Fifty U and solve them to find those bogus variables.
The other method is that the remaining elements are the multiplier coefficients because of which the respective positions became zero in the U matrix. (This method is a piddling catchy to understand by words but would go clear in the example beneath)
Now, we have A (the nXn coefficient matrix), L (the nXn lower triangular matrix), U (the nXn upper triangular matrix), X (the nX1 matrix of variables) and C (the nX1 matrix of numbers on the correct-hand side of the equations).
The given system of equations is A X = C. We substitute A = L U. Thus, nosotros have Fifty U Ten = C.
We put Z = U X, where Z is a matrix or artificial variables and solve for L Z = C first and then solve for U 10 = Z to find 10 or the values of the variables, which was required.

Example:
Solve the post-obit system of equations using LU Decomposition method:

$\begin{equation*} x_1 + x_2 + x_3 = 1 \end{equation*} \begin{equation*} 4x_1 + 3x_2 - x_3 = 6 \end{equation*} \begin{equation*} 3x_1 + 5x_2 + 3x_3 = 4 \end{equation*}$

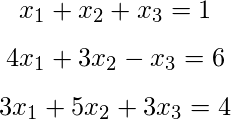
Solution: Here, we have

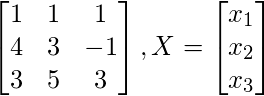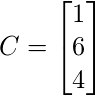A = $\begin{bmatrix} 1 & 1 & 1 \\ 4 & 3 & -1 \\ 3 & 5 & 3 \end{bmatrix} , X = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$ and $C = \begin{bmatrix} 1 \\ 6 \\ 4 \end{bmatrix}$ such that A X = C.

At present, we first consider 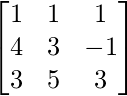$\begin{bmatrix} 1 & 1 & 1 \\ 4 & 3 & -1 \\ 3 & 5 & 3 \end{bmatrix}$ and convert it to row echelon form using Gauss Elimination Method.

Then, by doing

(i) $\begin{equation*} R_2 \to R_2 - 4R_1 \end{equation*}$

(2) $\begin{equation*} R_3 \to R_3 - 3R_1 \end{equation*}$

we get

$\begin{bmatrix} 1 & 1 & 1 \\ 4 & 3 & -1 \\ 3 & 5 & 3 \end{bmatrix} \sim$ $\begin{bmatrix} 1 & 1 & 1 \\ 0 & -1 & -5 \\ 0 & 2 & 0 \end{bmatrix}$

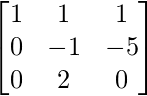
Now, by doing

(3) $\begin{equation*} R_3 \to R_3 - (-2)R_2 \end{equation*}$

we get

$\sim \begin{bmatrix} 1 & 1 & 1 \\ 0 & -1 & -5 \\ 0 & 0 & -10 \end{bmatrix}$

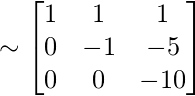
(Retrieve to e'er keep ' – ' sign in between, replace ' + ' sign past two ' – ' signs)

Hence, we get L = 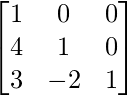$\begin{bmatrix} 1 & 0 & 0 \\ 4 & 1 & 0 \\ 3 & -2 & 1 \end{bmatrix}$ and U =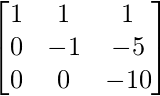 $\begin{bmatrix} 1 & 1 & 1 \\ 0 & -1 & -5 \\ 0 & 0 & -10 \end{bmatrix}$

(discover that in L matrix, $l_{21} = 4$ is from (1), $l_{31} = 3$ is from (2) and $l_{32} = -2$ is from (3))

At present, nosotros presume Z $= \begin{bmatrix} z_1 \\ z_2 \\ z_3 \end{bmatrix}$ and solve L Z = C.

$\begin{bmatrix} 1 & 0 & 0 \\ 4 & 1 & 0 \\ 3 & -2 & 1 \end{bmatrix} \begin{bmatrix} z_1 \\ z_2 \\ z_3 \end{bmatrix}$ $= \begin{bmatrix} 1 \\ 6 \\ 4 \end{bmatrix}$

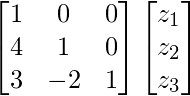
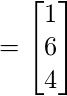
So, we accept $z_1 = 1 ,$ $4z_1 + z_2 = 6 ,$ $3z_1 - 2z_2 + z_3 = 4 .$

Solving, we get $z_1 = 1$ , $z_2 = 2$ and $z_3 = 5$ .

At present, we solve U 10 = Z

$\begin{bmatrix} 1 & 1 & 1 \\ 0 & -1 & -5 \\ 0 & 0 & -10 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix}$ $= \begin{bmatrix} 1 \\ 2 \\ 5 \end{bmatrix}$

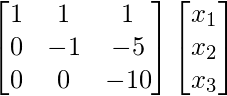
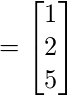
Therefore, we get $x_1 + x_2 + x_3 = 1 ,$ $-x_2 - 5x_3 = 2$ , $-10x_3 = 5 .$

Thus, the solution to the given organisation of linear equations is $x_1 = 1$ , $x_2 = 0.5$ , $x_3 = -0.5$ and hence the matrix X = $\begin{bmatrix} 1 \\ 0.5 \\ -0.5 \end{bmatrix}$

Exercise:
In the LU decomposition of the matrix

| two  2 | | 4  9 |

, if the diagonal elements of U are both 1, so the lower diagonal entry l22 of 50 is (GATE CS 2015)
(A) 4
(B) 5
(C) 6
(D) vii
For Solution, meet https://www.geeksforgeeks.org/gate-gate-cs-2015-set-1-question-28/

This article is compiled by Nishant Arora. Please write comments if yous find anything incorrect, or you desire to share more information about the topic discussed above.

pottergonell.blogspot.com

Source: https://www.geeksforgeeks.org/l-u-decomposition-system-linear-equations/

Can All Matrices a Ã¢ë†ë† R^nãƒâ€”n Be Factored a = Lu

0 Response to "Can All Matrices a Ã¢ë†ë† R^nãƒâ€”n Be Factored a = Lu"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel